Il triangolo è un poligono molto speciale. E ha delle caratteristiche utili.
Ad esempio la somma degli angoli interni di un triangolo totalizza SEMPRE un angolo piatto, cioè 180° oppure pi-greco, qualsiasi forma abbia il triangolo.
Vediamo come ciò può essere possibile:
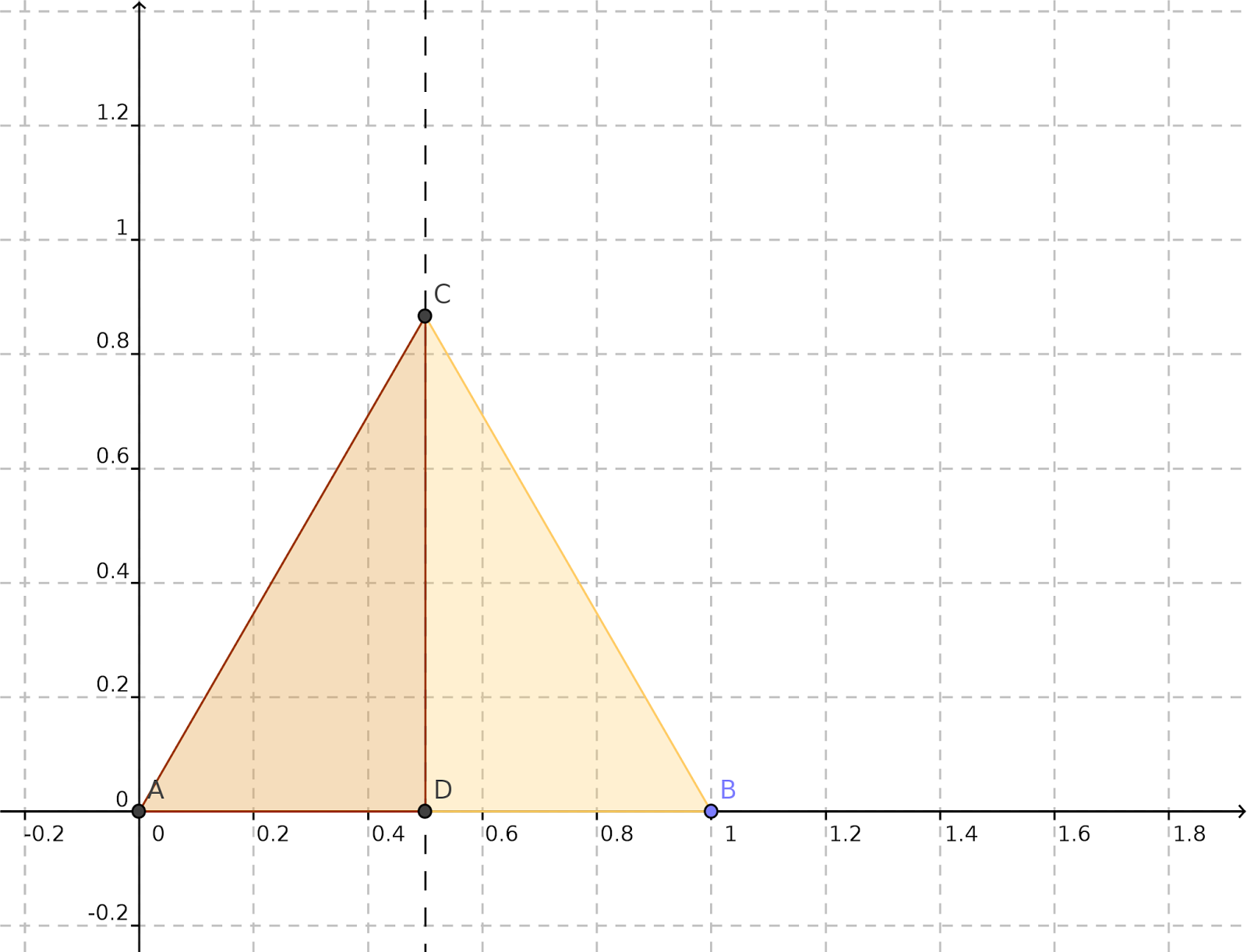
tracciamo una retta parallela al lato BC passante per il vertice A.
Abbiamo così due parallele (BC e AD) tagliate da una trasversale AC:
gli angoli tracciati in ROSSO sono angoli alterni interni e quindi sono uguali (congruenti).
Mantenendo le stesse parallele, se consideriamo ora come trasversale AB,
vediamo che gli angoli tracciati in VERDE sono angoli corrispondenti e quindi uguali (congruenti).
Con questa costruzione abbiamo "messo vicini" gli angoli interni di un triangolo, e vediamo subito che la loro somma è un angolo piatto!
venerdì 20 giugno 2014
martedì 10 giugno 2014
Problema dei due giardinieri
Il giardiniere Giorgio impiega 3 ore a tagliare l'erba di un certo prato, se lavora da solo.
Il suo collega, Enrico, impiega 1 ora a fare quel lavoro, se lavora da solo.
Quanto impiegano per il taglio di quel prato, se lavorano insieme?
RISPOSTA
Cominciamo dall'inizio.
Il problema è presentato in un modo che non permette di operare subito con i dati forniti: dobbiamo prima trasformarli. Un po' come succede con le frazioni, che vanno prima portate al denominatore comune.
Trasformiamo il tempo di lavoro in una velocità di lavoro:
vuol dire che se Giorgio impiega 3 ore a tagliare l'erba di quel prato, allora in un'ora ne taglia 1/3 del totale;
e che se Enrico impiega 1 ora a tagliare l'erba, allora in un'ora taglia tutto il prato.
Bene, quindi Giorgio taglia 1/3 del prato in un'ora ed Enrico taglia l'intero prato in un'ora. Queste due quantità possono essere sommate: se lavorassero entrambi per un'ora, taglierebbero 1 + 1/3 del prato. Possiamo così già immaginare (ma forse l'avevamo intuito dall'inizio) che se lavorano insieme impiegano meno di un'ora a svolgere tutto il lavoro. Ma quanto impiegano?
Se in un'ora svolgono 1/3 + 1 = 4 /3 del lavoro, quanto impiegheranno a svolgerne i 3/3?
Se in un'ora svolgono i 4/3 del lavoro, allora in 15 minuti ne svolgono 1/3, e quindi per svolgerne i 3/3 (cioè l'intero lavoro) impegano 45 minuti.
Il suo collega, Enrico, impiega 1 ora a fare quel lavoro, se lavora da solo.
Quanto impiegano per il taglio di quel prato, se lavorano insieme?
RISPOSTA
Cominciamo dall'inizio.
Il problema è presentato in un modo che non permette di operare subito con i dati forniti: dobbiamo prima trasformarli. Un po' come succede con le frazioni, che vanno prima portate al denominatore comune.
Trasformiamo il tempo di lavoro in una velocità di lavoro:
vuol dire che se Giorgio impiega 3 ore a tagliare l'erba di quel prato, allora in un'ora ne taglia 1/3 del totale;
e che se Enrico impiega 1 ora a tagliare l'erba, allora in un'ora taglia tutto il prato.
Bene, quindi Giorgio taglia 1/3 del prato in un'ora ed Enrico taglia l'intero prato in un'ora. Queste due quantità possono essere sommate: se lavorassero entrambi per un'ora, taglierebbero 1 + 1/3 del prato. Possiamo così già immaginare (ma forse l'avevamo intuito dall'inizio) che se lavorano insieme impiegano meno di un'ora a svolgere tutto il lavoro. Ma quanto impiegano?
Se in un'ora svolgono 1/3 + 1 = 4 /3 del lavoro, quanto impiegheranno a svolgerne i 3/3?
Se in un'ora svolgono i 4/3 del lavoro, allora in 15 minuti ne svolgono 1/3, e quindi per svolgerne i 3/3 (cioè l'intero lavoro) impegano 45 minuti.
lunedì 9 giugno 2014
Le dimensioni geometriche e fisiche
In geometria Euclide afferma che il punto è ciò che non ha parti. E' cioè senza dimensioni, cioè è un'entità geometrica a zero dimensioni.
La retta ha una dimensione (così anche il segmento, che è una parte di retta).
Il piano ha due dimensioni.
Lo spazio ha tre dimensioni.
Questo ha delle conseguenze dal punto di vista pratico, quando misuro ad esempio il volume di un solido o di un liquido.
Se voglio calcolare il volume di una scatola devo moltiplicare tra loro le tre dimensioni di cui è costituita.
Per misurarne le dimensioni, misuro gli spigoli: altezza, larghezza, profondità.
Ciascuno di essi è misurato in UNA dimensione, e l'unità di misura può essere ad esempio in metri.
Per calcolare la superficie di base moltiplico tra loro le misure degli spigoli di base, ottenendo una misura in metri quadrati,
infatti metri x metri = metri quadrati.
Infine, per calcolarne il volume moltiplico la superficie di base per la misura dello spigolo di altezza, ottenendo una misura espressa in metri cubi,
metri quadrati x metri = metri cubi.
In formula:
La retta ha una dimensione (così anche il segmento, che è una parte di retta).
Il piano ha due dimensioni.
Lo spazio ha tre dimensioni.
Questo ha delle conseguenze dal punto di vista pratico, quando misuro ad esempio il volume di un solido o di un liquido.
Se voglio calcolare il volume di una scatola devo moltiplicare tra loro le tre dimensioni di cui è costituita.
Per misurarne le dimensioni, misuro gli spigoli: altezza, larghezza, profondità.
Ciascuno di essi è misurato in UNA dimensione, e l'unità di misura può essere ad esempio in metri.
Per calcolare la superficie di base moltiplico tra loro le misure degli spigoli di base, ottenendo una misura in metri quadrati,
infatti metri x metri = metri quadrati.
Infine, per calcolarne il volume moltiplico la superficie di base per la misura dello spigolo di altezza, ottenendo una misura espressa in metri cubi,
metri quadrati x metri = metri cubi.
In formula:
sabato 7 giugno 2014
Le squadre da disegno... ma sono triangoli rettangoli!!?
Le squadre da disegno non sono triangoli rettangoli qualsiasi...
Questi sono trangoli rettangoli molto speciali.
Infatti gli angoli interni sono 30°, 60°, 90° per il primo triangolo
e 45°, 45°, 90° per il secondo.
Hai notato che il primo è la metà di un triangolo equilatero e
il secondo è la metà di un quadrato?
I lati hanno tra loro delle relazioni fisse:
nel primo il cateto più corto è sempre metà dell'ipotenusa,
nel secondo i due cateti sono della stessa lunghezza.
Vediamo il primo:
L'ipotenusa AC è un lato del triangolo equilatero,
il cateto CD è l'altezza del triangolo equilatero,
e il cateto AD è META' del lato del triangolo equilatero!
Passiamo al secondo:
I cateti AB e AC sono i lati del quadrato,
l'ipotenusa BC è la DIAGONALE del quadrato.
Non ci stupiamo ora se i due cateti sono uguali e se l'ipotenusa è radice di 2 volte la misura del cateto, come succede nei quadrati (in cui la diagonale è radice di 2 moltiplicato il lato).
Questi sono trangoli rettangoli molto speciali.
Infatti gli angoli interni sono 30°, 60°, 90° per il primo triangolo
e 45°, 45°, 90° per il secondo.
Hai notato che il primo è la metà di un triangolo equilatero e
il secondo è la metà di un quadrato?
I lati hanno tra loro delle relazioni fisse:
nel primo il cateto più corto è sempre metà dell'ipotenusa,
nel secondo i due cateti sono della stessa lunghezza.
Vediamo il primo:
il cateto CD è l'altezza del triangolo equilatero,
e il cateto AD è META' del lato del triangolo equilatero!
Passiamo al secondo:
I cateti AB e AC sono i lati del quadrato,
l'ipotenusa BC è la DIAGONALE del quadrato.
Non ci stupiamo ora se i due cateti sono uguali e se l'ipotenusa è radice di 2 volte la misura del cateto, come succede nei quadrati (in cui la diagonale è radice di 2 moltiplicato il lato).
Iscriviti a:
Post (Atom)